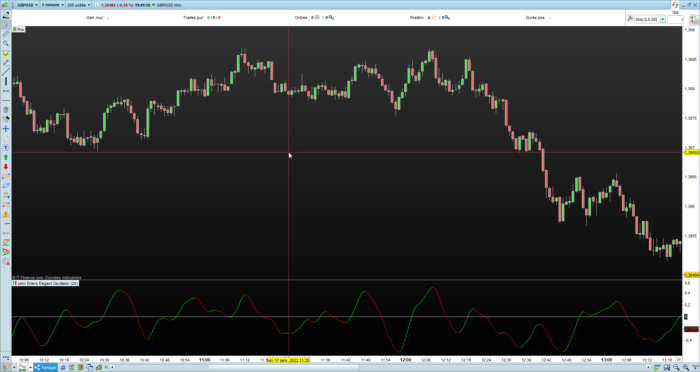
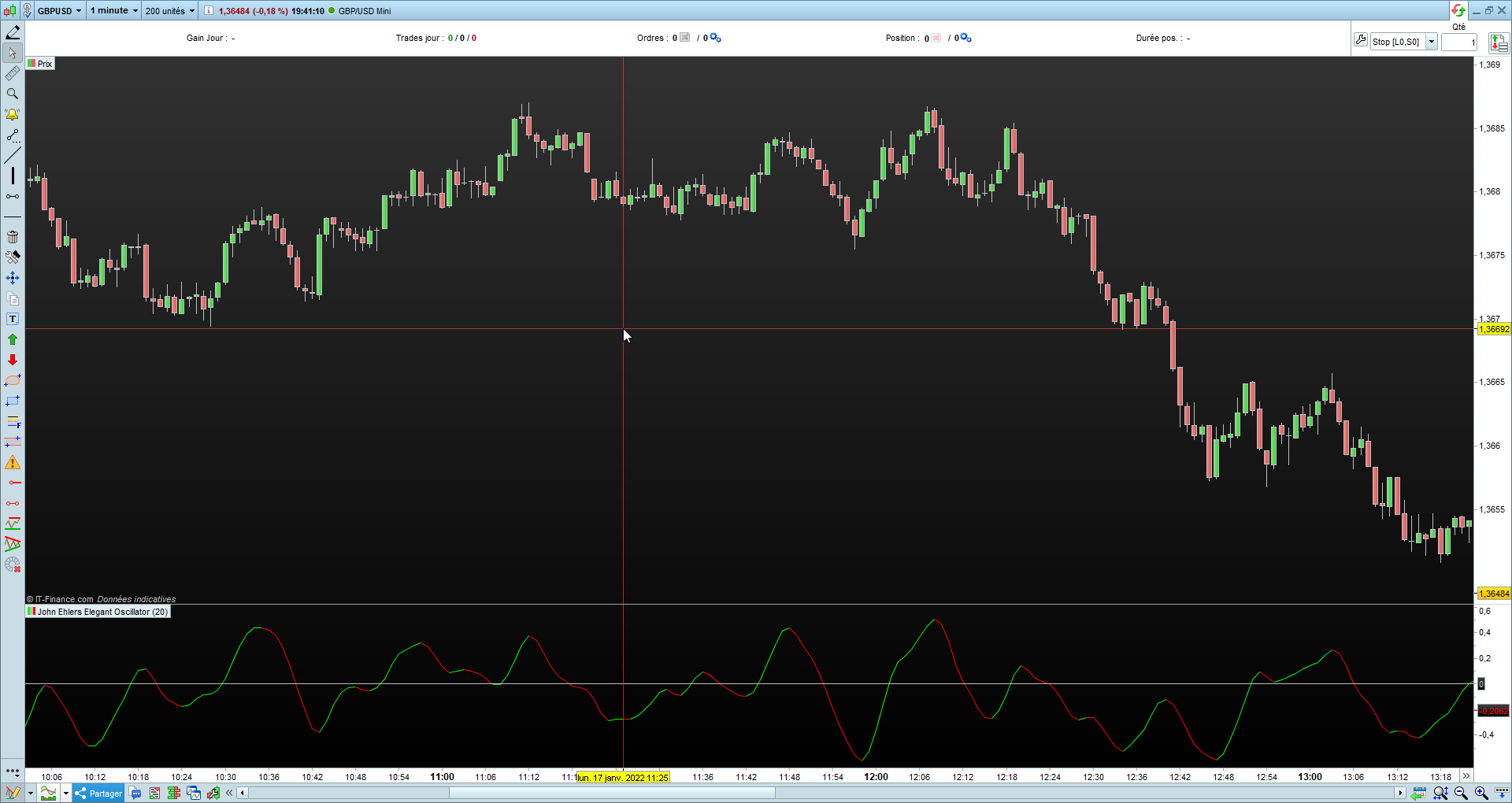
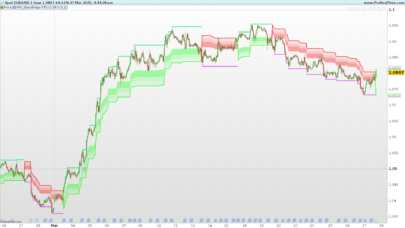
In his article in this issue, “An Elegant Oscillator: Inverse Fisher Transform Redux,” author John Ehlers explains how he uses the inverse Fisher transform to create an indicator he calls the elegant oscillator. First, he describes the Fisher transform before explaining the inverse Fisher transform, which provides normalization by dividing the root mean square (RMS) value into the waveform. The elegant oscillator can be used to spot reversion-to-the-mean opportunities with improved timing capabilities.

//Indicator:  TASC FEB 2022 Elegant Oscillator
//{
//TASC FEB 2022
//The Elegant Oscillator
//(c) 2021 John F. Ehlers
//}

// Parameters:
BandEdge: 20

//Take the derivative of prices
Deriv = Close - Close[2]
//Normalize to standard deviation
RMS = 0

for count = 0 to 49 do
RMS = RMS + Deriv[count]*Deriv[count]
next

if RMS <> 0 then
RMS = sqrt(RMS / 50)
endif
 
NDeriv = Deriv / RMS

//Compute the Inverse Fisher Transform
IFish = (exp(2*NDeriv) - 1) / (exp(2*NDeriv) + 1)

//Integrate with SuperSmoother
once a1 = exp(-1.414*3.14159 / BandEdge)
once b1 = 2*a1*cos(1.414*180 / BandEdge)
once c2 = b1
once c3 = -a1*a1
once c1 = 1 - c2 - c3

if barindex < 50 + BandEdge then
SS = 0
else
SS = c1*(IFish + IFish[1]) / 2 + c2*SS[1] + c3*SS[2]
endif
 
return SS, 0